The corresponding altitudes of two similar triangles are 6 cm and 9 cm respectively.

Let the two triangles be ABC and DEF with altitudes AP and DQ, respectively​.

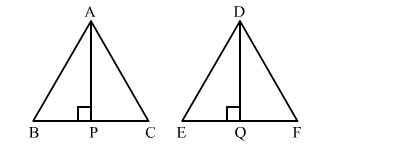
It is given that $\triangle A B C \sim \triangle D E F$.

We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding altitudes. 

$\therefore \frac{\operatorname{ar}(\triangle A B C)}{\operatorname{ar}(\triangle D E F)}=\frac{(A P)^{2}}{(D Q)^{2}}$

$\Rightarrow \frac{\operatorname{ar}(\triangle A B C)}{\operatorname{ar}(\triangle D E F)}=\frac{6^{2}}{9^{2}}$

$=\frac{36}{81}$

$=\frac{4}{9}$

Hence, the ratio of their areas is 4 : 9