The diagonals of a cyclic quadrilateral are at right angles.

Let ABCD be a cyclic quadrilateral whose diagonals AC and BD intersect at O at right angles.
Let OL ⊥ AB such that LO produced meets CD at M.

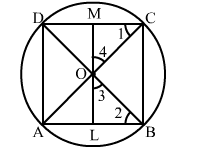
Then we have to prove that CM = MD
Clearly, ∠1 = ∠2   [Angles in the same segment]
∠2 + ∠3 = 90°   [∵ ∠OLB = 90°]
∠3 + ∠4= 90°    [∵ LOM is a straight line and ∠BOC = 90°]
∴ ∠2 + ∠3  = ∠3 + ∠4 ⇒∠2 = ∠4
Thus, ∠1 = ∠2 and ∠2 = ∠4 ⇒ ∠1 = ∠4
∴ OM = CM and, similarly, OM =  MD
Hence, CM =  MD