The diagonals of quadrilateral ABCD intersect at O. Prove that

Solution:

We are given the following quadrilateral with O as the intersection point of diagonals

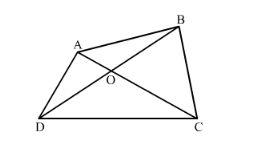
To Prove: $\frac{\operatorname{ar}(\Delta A C B)}{\operatorname{ar}(\triangle A C D)}=\frac{B O}{D O}$

Given ACB and ACD are two triangles on the same base AC

Consider h as the distance between two parallel sides

Now we see that the height of these two triangles ACB and ACD are same and are equal to h

So

$\frac{\operatorname{ar}(A C B)}{\operatorname{ar}(A C D)}=\frac{\frac{1}{2} \times A B \times h}{\frac{1}{2} \times C D \times h}$

=\frac{A B}{C D}...(1)

Now consider the triangles AOB and COD in which

$\angle A O B=\angle C O D$

$\angle A B O=\angle O D C$(alternative angle)

 

$\angle B A O=\angle D C A$(alternative angle)

Therefore, $\triangle O D C \sim \triangle O B A$

$\Rightarrow \frac{A O}{O C}=\frac{B O}{D O}=\frac{A B}{C D}$

$\Rightarrow \frac{B O}{D O}=\frac{A B}{C D}$...(2)

From equation (1) and (2) we get

$\frac{a r(A C B)}{a r(A C D)}=\frac{B O}{D O}$

Hence prove that $\frac{a r(\triangle A C B)}{a r(\triangle A C D)}=\frac{B O}{D O}$