The diameters of the top and the bottom portions

Radius of top of bucket $r_{1}=\frac{42}{2}=21 \mathrm{~cm}$

Radius of bottom of bucket $r_{2}=\frac{28}{2}=14 \mathrm{~cm}$

Height of bucket, $h=24 \mathrm{~cm}$.

$I=\sqrt{h^{2}\left(r_{1}-r_{2}\right)}$

$=\sqrt{576+(21-14)^{2}}$

$=\sqrt{576+49}$

$=\sqrt{625}$

$=25$

C.S.A. of the bucket

$=\pi\left(r_{1}+r_{2}\right) l$

$=\pi(21+14) \times 25$

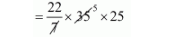
= 2750 cm2

Area of bottom

$=\pi r^{2}$

$=\frac{22}{7} \times 196$

$=616 \mathrm{~cm}^{2}$

The cost of painting its C.S. ,

$=(2750+616) \times \frac{1}{2}$

$=3366 \times \frac{1}{2}$

$=\operatorname{Rs} 1683$

Hence, the correct answer is choice (c).