Question:
The digits of a 3 - digit number are in AP, and their sum is 15. The number obtained by reversing the digits is 594 less than the original number. Find the number.
Solution:
To Find: The number
Given: The digits of a 3 – digit number are in AP, and their sum is 15.
Let required digit of 3 - digit number be (a - d), (a), (a + d). Then,
$(a-d)+(a)+(a+d)=15 \Rightarrow 3 a=15 \Rightarrow a=5$
(Figure show 3 digit number original number)
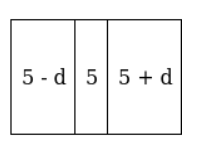
(Figure show 3 digit number in reversing form)
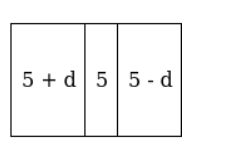
So, $(5+d) \times 100+5 \times 10+(5-d) \times 1=\{(5-d) \times 100+5 \times 10+(5+d) \times 1\}-594$
$200 d-2 d=-594 \Rightarrow d=-3$ and $a=5$
So the original number is 852