The distance (in km) of 40 engineers from their residence to their place of work were found as follows.
Question.
The distance (in km) of 40 engineers from their residence to their place of work were found as follows.
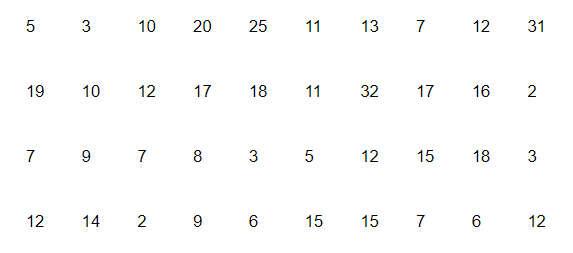
What is the empirical probability that an engineer lives:
(i) less than 7 km from her place of work?
(ii) more than or equal to 7 km from her place of work?
(iii) within $\frac{1}{2} \mathrm{~km}$ from her place of work?
The distance (in km) of 40 engineers from their residence to their place of work were found as follows.
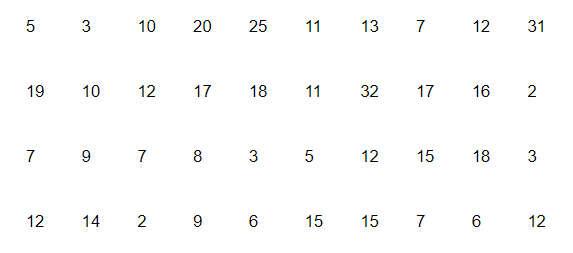
What is the empirical probability that an engineer lives:
(i) less than 7 km from her place of work?
(ii) more than or equal to 7 km from her place of work?
(iii) within $\frac{1}{2} \mathrm{~km}$ from her place of work?
Solution:
(i) Total number of engineers = 40
Number of engineers living less than 7 km from their place of work = 9
Hence, required probability that an engineer lives less than $7 \mathrm{~km}$ from her place of work, $\mathrm{P}=\frac{9}{40}$
(ii) Number of engineers living more than or equal to 7 km from their place of work = 40 − 9 = 31
Hence, required probability that an engineer lives more than or equal to $7 \mathrm{~km}$ from her place of work, $\mathrm{P}=\frac{31}{40}$
(iii) Number of engineers living within $\frac{1}{2} \mathrm{~km}$ from her place of work $=0$
Hence, required probability that an engineer lives within $\frac{1}{2} \mathrm{~km}$ from her place of work, $P=0$
(i) Total number of engineers = 40
Number of engineers living less than 7 km from their place of work = 9
Hence, required probability that an engineer lives less than $7 \mathrm{~km}$ from her place of work, $\mathrm{P}=\frac{9}{40}$
(ii) Number of engineers living more than or equal to 7 km from their place of work = 40 − 9 = 31
Hence, required probability that an engineer lives more than or equal to $7 \mathrm{~km}$ from her place of work, $\mathrm{P}=\frac{31}{40}$
(iii) Number of engineers living within $\frac{1}{2} \mathrm{~km}$ from her place of work $=0$
Hence, required probability that an engineer lives within $\frac{1}{2} \mathrm{~km}$ from her place of work, $P=0$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
