The distance of the point (-1,2,-2)

$P_{1}: 2 x+3 y+2 z=0$

$\Rightarrow \overrightarrow{\mathrm{n}}_{1}=2 \hat{\mathrm{i}}+3 \hat{\mathrm{j}}+2 \hat{\mathrm{k}}$

$P_{2}: x-2 y+z=0$

$\Rightarrow \overrightarrow{\mathrm{n}}_{2}=\hat{\mathrm{i}}-2 \hat{\mathrm{j}}+\mathrm{k}$

Direction vector of line $L$ which is line of intersection of $P_{1} \& P_{2}$

$\overrightarrow{\mathrm{r}}=\overrightarrow{\mathrm{n}}_{1} \times \overrightarrow{\mathrm{n}}_{2}=7 \hat{\mathrm{i}}-7 \hat{\mathrm{k}}$

DR's of $L$ are $(1,0,-1)$

$\Rightarrow$ Equation of $L: \frac{x}{1}=\frac{y}{0}=\frac{z}{-1}=\lambda$

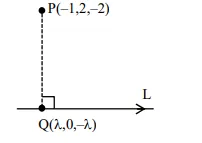
DR's of $\overrightarrow{\mathrm{PQ}}=(\lambda+1,-2,2-\lambda)$

$\because \overline{\mathrm{PQ}} \perp \overrightarrow{\mathrm{r}}$

$\Rightarrow(\lambda+1)(1)+(-2)(0)+(2-\lambda)(-1)=0$

$\Rightarrow \lambda=\frac{1}{2} \Rightarrow Q\left(\frac{1}{2}, 0, \frac{-1}{2}\right)$

$\Rightarrow \mathrm{PQ}=\frac{\sqrt{34}}{2}$