The driver of a car travelling at 52 km h–1 applies the brakes and accelerates uniformly in the opposite direction.
Question.
The driver of a car travelling at 52 km h–1 applies the brakes and accelerates uniformly in the opposite direction. The car stops in 5 s. Another driver going at 3 kmh–1 in another car, applies his brakes slowly and stops in 10 s. On the same graph paper, plot the speed versus time graphs for the two cars. Which of the two cars travelled farther after the brakes were applied ?
The driver of a car travelling at 52 km h–1 applies the brakes and accelerates uniformly in the opposite direction. The car stops in 5 s. Another driver going at 3 kmh–1 in another car, applies his brakes slowly and stops in 10 s. On the same graph paper, plot the speed versus time graphs for the two cars. Which of the two cars travelled farther after the brakes were applied ?
Solution:
The speed time graph of both the cars are shown below.
(i) Distance covered by car moving at $52 \mathrm{kmh}^{-1}$
(or $52 \times \frac{5}{18}=14.4 \mathrm{~ms}^{-1}$ )
$=$ area of $\Delta \mathrm{POQ}=\frac{1}{2} \times \mathrm{PO} \times \mathrm{OQ}=\frac{1}{2} \times 14.4 \times 5=36 \mathrm{~m}$
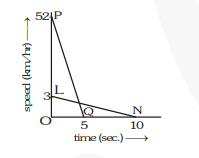
(ii) Distance covered by car moving at $3 \mathrm{kmh}^{-1}$
$\left(\right.$ or $\left.3 \times \frac{5}{18}=0.83 \mathrm{~ms}^{-1}\right)$
$=$ area of $\Delta \mathrm{OLN}=\frac{1}{2} \times \mathrm{LO} \times \mathrm{ON}=\frac{1}{2} \times 0.83 \times 10$
$=4.15 \mathrm{~m}$
$\therefore$ The car moving at $52 \mathrm{~km} \mathrm{~h}^{-1}$ travels more distance on the application of brakes.
The speed time graph of both the cars are shown below.
(i) Distance covered by car moving at $52 \mathrm{kmh}^{-1}$
(or $52 \times \frac{5}{18}=14.4 \mathrm{~ms}^{-1}$ )
$=$ area of $\Delta \mathrm{POQ}=\frac{1}{2} \times \mathrm{PO} \times \mathrm{OQ}=\frac{1}{2} \times 14.4 \times 5=36 \mathrm{~m}$

(ii) Distance covered by car moving at $3 \mathrm{kmh}^{-1}$
$\left(\right.$ or $\left.3 \times \frac{5}{18}=0.83 \mathrm{~ms}^{-1}\right)$
$=$ area of $\Delta \mathrm{OLN}=\frac{1}{2} \times \mathrm{LO} \times \mathrm{ON}=\frac{1}{2} \times 0.83 \times 10$
$=4.15 \mathrm{~m}$
$\therefore$ The car moving at $52 \mathrm{~km} \mathrm{~h}^{-1}$ travels more distance on the application of brakes.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
