The fig. depicts an archery target marked with its five scoring regions from the centre outwards as Gold,
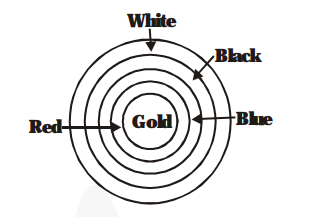
The fig. depicts an archery target marked with its five scoring regions from the centre outwards as Gold, Red, Blue, Black and White. The diameter of the region representing Gold score is 21 cm and each of the other bands is 10.5 cm wide. Find the area of each of the five scoring regions.
Radius of the Gold scoring region
$=\frac{21}{2} \mathrm{~cm}=10.5 \mathrm{~cm}(\because$ Diameter $=21 \mathrm{~cm})$
Therefore, the area of the Gold scoring region (circle)
$=\pi \times\left(\frac{21}{2}\right)^{2} \mathrm{~cm}^{2}=\frac{22}{7} \times \frac{21}{2} \times \frac{21}{2} \mathrm{~cm}^{2}$
$=\frac{\mathbf{3 3} \times \mathbf{2 1}}{\mathbf{2}} \mathbf{c m}^{\mathbf{2}}=\frac{\mathbf{6 9 3}}{\mathbf{2}} \mathbf{c m}^{\mathbf{2}}=346.5 \mathrm{~cm}^{2}$
Radius of the combined circular region scoring Gold and Red
= radius of Gold scoring region
width of the Red scoring band
= 10.5 cm + 10.5 cm = 21 cm
The area of the Red scoring region
= Combined area of Gold and Red scoring region – area of Gold scoring region.
$=\left\{\pi \times(21)^{2}-\pi \times\left(\frac{21}{2}\right)^{2}\right\} \mathrm{cm}^{2}$
$=\pi \times\left\{(21)^{2}-\left(\frac{21}{2}\right)^{2}\right\} \mathrm{cm}^{2}$
$=\frac{22}{7} \times\left\{\left(\frac{21}{2} \times 2\right)^{2}-\left(\frac{21}{2}\right)^{2}\right\} \mathrm{cm}^{2}$
$=\frac{22}{7} \times\left(\frac{21}{2}\right)^{2} \times\{4-1\} \mathrm{cm}^{2}=\frac{22}{7} \times \frac{21}{2} \times \frac{21}{2} \times 3 \mathrm{~cm}^{2}$
$=\frac{\mathbf{6 9 3}}{\mathbf{2}} \times \mathbf{3} \mathbf{c m}^{2}=\frac{\mathbf{2 0 7 9}}{\mathbf{2}} \mathbf{c m}^{2}=1039.5 \mathrm{~cm}^{2}$
Radius of the combined circular region scoring Gold, Red and Blue.
= 10.5 cm + 10.5 cm + 10.5 cm = 31.5 cm
$=\frac{\mathbf{6 3}}{\mathbf{2}} \mathrm{cm}$
Then, area of the Blue scoring region = {Combined area of Gold, Red and Blue scoring regions}
– {Combined area of Gold and Red scoring regions}
$=\pi \times\left(\frac{\mathbf{6 3}}{\mathbf{2}}\right)^{\mathbf{2}}-\pi \times(21)^{2}=\pi \times(21)^{2} \times\left\{\frac{\mathbf{9}}{\mathbf{4}}-\mathbf{1}\right\}$
$=\frac{22}{7} \times 21 \times 21 \times \frac{5}{4} \mathrm{~cm}^{2}=\frac{11 \times 63 \times 5}{2} \mathrm{~cm}^{2}$
$=1732.5 \mathrm{~cm}^{2}$
Similarly, we find the area of the black scoring region
$=\left\{\pi \times(31.5+10.5)^{2}-\pi \times(31.5)^{2}\right\} \mathrm{cm}^{2}$
$=\left\{\pi \times(42)^{2}-\pi \times\left(\frac{63}{2}\right)^{2}\right\} \mathrm{cm}^{2}$
$=\pi \times(21)^{2} \times\left\{4-\frac{9}{4}\right\} \mathrm{cm}^{2}=\frac{22}{7} \times 21 \times 21 \times \frac{7}{4} \mathrm{~cm}^{2}$
$=\frac{231 \times 21}{2} \mathbf{c m}^{2}=\frac{4851}{2} \mathbf{c m}^{2}=2425.5 \mathrm{~cm}^{2}$
Now, the area of the white scoring region
$=\left\{\pi \times(42+10.5)^{2}-\pi \times(42)^{2}\right\} \mathrm{cm}^{2}$
$=\left\{\pi \times\left(\frac{105}{2}\right)^{2}-\pi \times(42)^{2}\right\} \mathrm{cm}^{2}$$=\pi \times(21)^{2} \times\left\{\frac{25}{4}-4\right\} c m^{2}$
$=\frac{22}{7} \times 21 \times 21 \times \frac{9}{4} \mathrm{~cm}^{2}$
$=\frac{6237}{2} \mathbf{m m}^{2}=3118.5 \mathrm{~cm}^{2}$
