The focus of a parabolic mirror is at a distance of 6 cm from its vertex

Given: The focus of a parabolic mirror is at a distance of 6 cm from its vertex. And the mirror is 20 cm deep.

Need to find: Diameter of the mirror

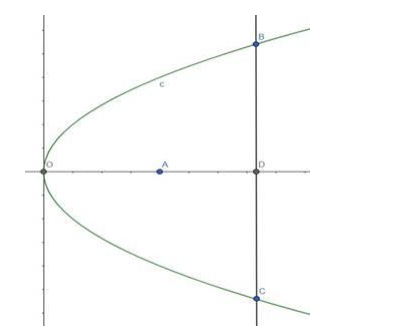
Here $O$ is the vertex and $A$ is the Focus. So, $O A=a=6 \mathrm{~cm}$.

OD is the deep of the mirror $=20 \mathrm{~cm}$

$B C$ is the diameter of the mirror.

Equation of the parabola is, $\mathrm{y}^{2}=4 \mathrm{ax}$

$\Rightarrow y^{2}=24 x$

The mirror is $20 \mathrm{~cm}$ deep. That means the $x$-coordinate of the points $B, C$ and $D$ is 20

Both the points, B and C are on the parabola. Hence, the points satisfies the equation of the parabola.

Therefore, $y^{2}=24 \times 20=480$

$\Rightarrow y=\pm 21.9$

So, the coordinate of $B$ is $(20,21.9)$ and the coordinate of $C$ is $(20,-21.9)$.

Therefore, the diameter of the mirror is $=(21.9+21.9) \mathrm{cm}$

$=43.8 \mathrm{~cm}$