The following data are obtained when dinitrogen and dioxygen react together to form different compounds
Question.
The following data are obtained when dinitrogen and dioxygen react together to form different compounds
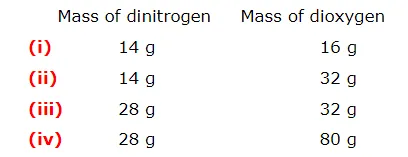
(a)Which law of chemical combination is obeyed by the above experimental data?Give its statement
(b)Fill in the blanks in the following conversions
(i) $\quad 1 \mathrm{~km}=\ldots \ldots \ldots \ldots \ldots \ldots . \mathrm{mm}=\ldots \ldots \ldots \ldots \ldots \ldots . \mathrm{pm}$
(ii) $1 \mathrm{mg}=\ldots \ldots \ldots \ldots \ldots \ldots \ldots \mathrm{kg}=\ldots \ldots \ldots \ldots \ldots \ldots \ldots \mathrm{ng}$
(iii) $\quad 1 \mathrm{~mL}=\ldots \ldots \ldots \ldots \ldots \ldots . \mathrm{L}=\ldots \ldots \ldots \ldots \ldots \ldots . \mathrm{dm}^{3}$
The following data are obtained when dinitrogen and dioxygen react together to form different compounds

(a)Which law of chemical combination is obeyed by the above experimental data?Give its statement
(b)Fill in the blanks in the following conversions
(i) $\quad 1 \mathrm{~km}=\ldots \ldots \ldots \ldots \ldots \ldots . \mathrm{mm}=\ldots \ldots \ldots \ldots \ldots \ldots . \mathrm{pm}$
(ii) $1 \mathrm{mg}=\ldots \ldots \ldots \ldots \ldots \ldots \ldots \mathrm{kg}=\ldots \ldots \ldots \ldots \ldots \ldots \ldots \mathrm{ng}$
(iii) $\quad 1 \mathrm{~mL}=\ldots \ldots \ldots \ldots \ldots \ldots . \mathrm{L}=\ldots \ldots \ldots \ldots \ldots \ldots . \mathrm{dm}^{3}$
Solution:
(a)
If we fix the mass of dinitrogen at 28 g, then the masses of dioxygen that will combine with the fixed mass of dinitrogen are 32 g, 64 g, 32 g, and 80 g
The masses of dioxygen bear a whole number ratio of 1:2:2:5. Hence, the given experimental data obeys the law of multiple proportions. The law states that if two elements combine to form more than one compound, then the masses of one element that combines with the fixed mass of another element are in the ratio of small whole numbers
(b) (i) $1 \mathrm{~km}=1 \mathrm{~km} \times \frac{1000 \mathrm{~m}}{1 \mathrm{~km}} \times \frac{100 \mathrm{~cm}}{1 \mathrm{~m}} \times \frac{10 \mathrm{~mm}}{1 \mathrm{~cm}}$
$\therefore 1 \mathrm{~km}=10^{6} \mathrm{~mm}$
$1 \mathrm{~km}=1 \mathrm{~km} \times \frac{1000 \mathrm{~m}}{1 \mathrm{~km}} \times \frac{1 \mathrm{pm}}{10^{-12} \mathrm{~m}}$
$\therefore 1 \mathrm{~km}=10^{15} \mathrm{pm}$
Hence, $1 \mathrm{~km}=10^{6} \mathrm{~mm}=10^{15} \mathrm{pm}$
(ii) $1 \mathrm{mg}=1 \mathrm{mg} \frac{1 \mathrm{~g}}{1000 \mathrm{mg}} \times \frac{1 \mathrm{~kg}}{1000 \mathrm{~g}} \times$
$\Rightarrow 1 \mathrm{mg}=10^{-6} \mathrm{~kg}$
$1 \mathrm{mg}=1 \mathrm{mg} \times \frac{1 \mathrm{~g}}{1000 \mathrm{mg}} \times \frac{1 \mathrm{ng}}{10^{-9} \mathrm{~g}}$
$\Rightarrow 1 \mathrm{mg}=10^{6} \mathrm{ng}$
$\therefore 1 \mathrm{mg}=10^{-6} \mathrm{~kg}=10^{6} \mathrm{ng}$
(iii) $1 \mathrm{~mL}=1 \mathrm{~mL} \times \frac{1 \mathrm{~L}}{1000 \mathrm{~mL}}$
$\Rightarrow 1 \mathrm{~mL}=10^{-3} \mathrm{~L}$
$1 \mathrm{~mL}=1 \mathrm{~cm}^{3}=1 \frac{1 \mathrm{dm} \times 1 \mathrm{dm} \times 1 \mathrm{dm}}{10 \mathrm{~cm} \times 10 \mathrm{~cm} \times 10 \mathrm{~cm}} \mathrm{~cm}^{3}$
$\Rightarrow 1 \mathrm{~mL}=10^{-3} \mathrm{dm}^{3}$
$\therefore 1 \mathrm{~mL}=10^{-3} \mathrm{~L}=10^{-3} \mathrm{dm}^{3}$
(a)
If we fix the mass of dinitrogen at 28 g, then the masses of dioxygen that will combine with the fixed mass of dinitrogen are 32 g, 64 g, 32 g, and 80 g
The masses of dioxygen bear a whole number ratio of 1:2:2:5. Hence, the given experimental data obeys the law of multiple proportions. The law states that if two elements combine to form more than one compound, then the masses of one element that combines with the fixed mass of another element are in the ratio of small whole numbers
(b) (i) $1 \mathrm{~km}=1 \mathrm{~km} \times \frac{1000 \mathrm{~m}}{1 \mathrm{~km}} \times \frac{100 \mathrm{~cm}}{1 \mathrm{~m}} \times \frac{10 \mathrm{~mm}}{1 \mathrm{~cm}}$
$\therefore 1 \mathrm{~km}=10^{6} \mathrm{~mm}$
$1 \mathrm{~km}=1 \mathrm{~km} \times \frac{1000 \mathrm{~m}}{1 \mathrm{~km}} \times \frac{1 \mathrm{pm}}{10^{-12} \mathrm{~m}}$
$\therefore 1 \mathrm{~km}=10^{15} \mathrm{pm}$
Hence, $1 \mathrm{~km}=10^{6} \mathrm{~mm}=10^{15} \mathrm{pm}$
(ii) $1 \mathrm{mg}=1 \mathrm{mg} \frac{1 \mathrm{~g}}{1000 \mathrm{mg}} \times \frac{1 \mathrm{~kg}}{1000 \mathrm{~g}} \times$
$\Rightarrow 1 \mathrm{mg}=10^{-6} \mathrm{~kg}$
$1 \mathrm{mg}=1 \mathrm{mg} \times \frac{1 \mathrm{~g}}{1000 \mathrm{mg}} \times \frac{1 \mathrm{ng}}{10^{-9} \mathrm{~g}}$
$\Rightarrow 1 \mathrm{mg}=10^{6} \mathrm{ng}$
$\therefore 1 \mathrm{mg}=10^{-6} \mathrm{~kg}=10^{6} \mathrm{ng}$
(iii) $1 \mathrm{~mL}=1 \mathrm{~mL} \times \frac{1 \mathrm{~L}}{1000 \mathrm{~mL}}$
$\Rightarrow 1 \mathrm{~mL}=10^{-3} \mathrm{~L}$
$1 \mathrm{~mL}=1 \mathrm{~cm}^{3}=1 \frac{1 \mathrm{dm} \times 1 \mathrm{dm} \times 1 \mathrm{dm}}{10 \mathrm{~cm} \times 10 \mathrm{~cm} \times 10 \mathrm{~cm}} \mathrm{~cm}^{3}$
$\Rightarrow 1 \mathrm{~mL}=10^{-3} \mathrm{dm}^{3}$
$\therefore 1 \mathrm{~mL}=10^{-3} \mathrm{~L}=10^{-3} \mathrm{dm}^{3}$
