The following distribution shows the daily pocket allowance of children of a locality.

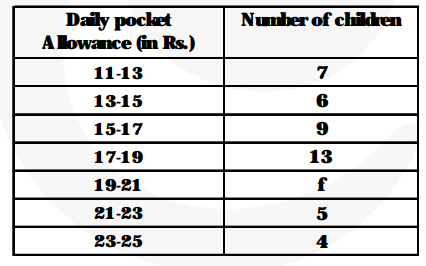
We may prepare the table as given below :

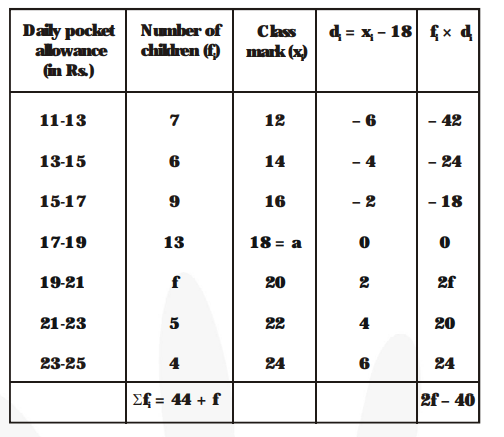
It is given that mean = 18.

From the table, we have

$\mathrm{a}=18, \mathrm{n}=44+\mathrm{f}$ and $\Sigma \mathrm{f}_{\mathrm{d}} \mathrm{d}=2 \mathrm{f}-40$

Now, mean $=\mathrm{a}+\frac{\mathbf{1}}{\mathbf{n}} \times \Sigma \mathrm{f}_{\mathrm{i}} \mathrm{d}_{\mathrm{i}}$

Then substituting the values as given above, we have

$18=18+\frac{\mathbf{1}}{\mathbf{( 4 4}+\mathbf{f})} \times(2 \mathrm{f}-40)$

$\Rightarrow \quad 0=\frac{\mathbf{2 f}-\mathbf{4 0}}{\mathbf{4 4}+\mathbf{f}} \Rightarrow \mathrm{f}=20$