The following frequency distribution gives the monthly consumption of electricity

The given data is shown below.

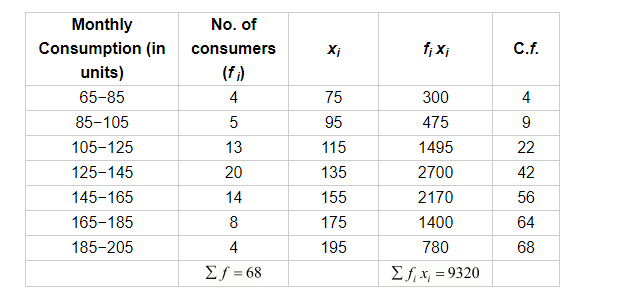
Here, the maximum frequency is 20 so the modal class is 125−145.

Therefore,

$l=125$

$h=20$

$f=20$

$f_{1}=13$

$f_{2}=14$

$\Rightarrow$ Mode $=l+\frac{f-f_{1}}{2 f-f_{1}-f_{2}} \times h$

$=125+\frac{7}{13} \times 20$

$=125+\frac{140}{13}$

Mode $=135.76$ units

Thus, the mode of the monthly consumption of electricity is 135.76 units.

Mean $=\frac{\sum f_{i} x_{i}}{\sum f}=\frac{9320}{68}=137.05$

Thus, the mean of the monthly consumption of electricity is 137.05 units.

Here,

Total number of consumers, $N=68$ (even)

Then, $\frac{N}{2}=34$

$\therefore$ Median

$=l+\frac{\frac{N}{2}-F}{f} \times h$

$=125+\frac{\frac{68}{2}-22}{20} \times 20$

$=125+\frac{34-22}{20} \times 20$

$=125+12$

$=137$

Thus, the median of the monthly consumption of electricity is 137 units.