The following is the frequency distribution

First, we calculate class marks as follows

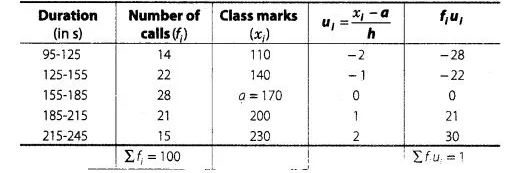
Here, (assumed mean) a = 170,

and (class width) h = 30

By step deviation method,

Average $(\bar{x})=a+\frac{\sum f_{i} u_{j}}{\sum f_{j}} \times h=170+\frac{1}{100} \times 30$

$=170+0.3=170.3$

Hence, average duration is 170.3s.

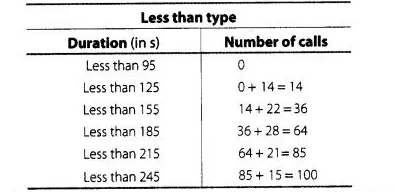
For calculating median from a cumulative frequency curve

We prepare less than type or more than type ogive

We observe that, number of calls in less than 95 s is 0. Similarly, in less than 125 s include the number of calls in less than 95 s as well as the

number of calls from 95-125.s So, the total number of calls less than 125 s is 0 + 14 = 14. Continuing in this manner, we will get remaining in less

than 155,185, 215 and 245 s.

Now, we construct a table for less than ogive (cumulative frequency curve).

To draw less than type ogive we plot them the points $(95,0),(125,14)(155,36),(185,64)$, $(215,85),(245,100)$ on the paper and join them by free hand.

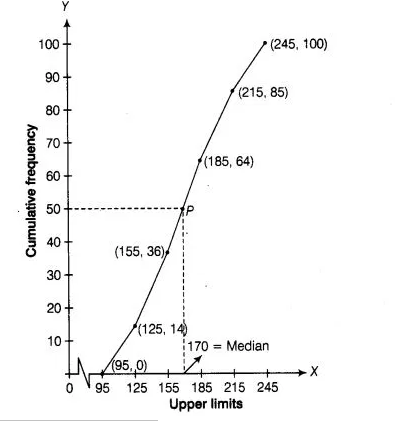
$\because$ Total number of calls $(n)=100$

$\therefore$ $\frac{n}{2}=\frac{100}{2}=50$

Now, point 50 taking on Y-axis draw a line parallel to X-axis meet at a point P and draw a perpendicular line from P to the X-axis, the intersection

point of X-axis is the median.

Hence, required median is 170 .