The following is the record of goals scored by team A in a football session:
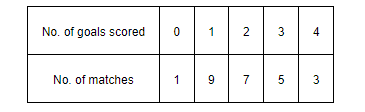
For the team B, mean number of goals scored per match was 2 with a standard
deviation 1.25 goals. Find which team may be considered more consistent?
The mean and the standard deviation of goals scored by team A are calculated as follows.
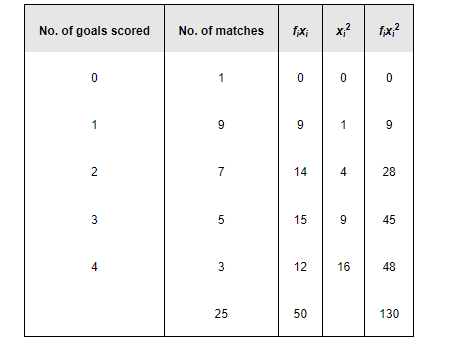
Mean $=\frac{\sum_{i=1}^{5} f_{i} x_{i}}{\sum_{i=1}^{5} f_{i}}=\frac{50}{25}=2$
Thus, the mean of both the teams is same.
$\sigma=\frac{1}{N} \sqrt{N \sum f_{i} x_{i}{ }^{2}-\left(\sum f_{i} x_{i}\right)^{2}}$
$=\frac{1}{25} \sqrt{25 \times 130-(50)^{2}}$
$=\frac{1}{25} \sqrt{750}$
$=\frac{1}{25} \times 27.38$
$=1.09$
The standard deviation of team B is 1.25 goals.
The average number of goals scored by both the teams is same i.e., 2. Therefore, the team with lower standard deviation will be more consistent.
Thus, team A is more consistent than team B.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
