Question:
The following results were obtained during kinetic studies of the reaction;
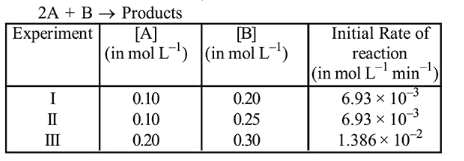
The time (in minutes) required to consume half of $\mathrm{A}$ is:
Correct Option: 1
Solution:
From experiment 1 and II, it is observed that order of reaction w.r.t. (3) is zero.
From experiment II and III, $\alpha$ can be calculated as:
$\frac{1.386 \times 10^{-2}}{6.93 \times 10^{-3}}=\left(\frac{0.2}{0.1}\right)^{\alpha}$
$\therefore \quad \alpha=1$
Now, $\quad$ Rate $=\mathrm{K}[\mathrm{A}]^{1}$
or, $6.93 \times 10^{-3}=K(0.1)$
$K=6.93 \times 10^{-2}$
For the reaction, $2 \mathrm{~A}+\mathrm{B} \rightarrow$ Products
$2 K t=\ln \frac{[\mathrm{A}]_{0}}{[\mathrm{~A}]}$
$\therefore \quad t_{1 / 2}=\frac{0.693}{2 K}=\frac{0.693}{0.693 \times 10^{-2} \times 2}$
$t_{1 / 2}=5$
