The frequency distribution:

Given frequency distribution table, where variance =160

Now we have to find the value of A, where A is a positive number

Now we have to construct a table of the given data

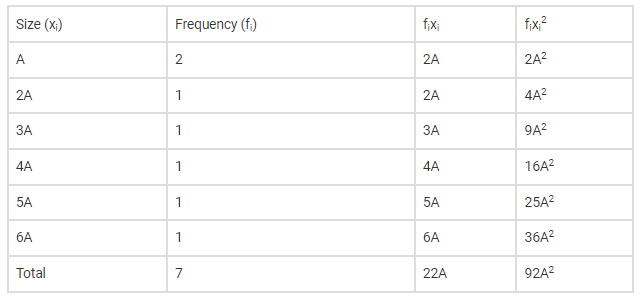
And we know variance is

$\sigma^{2}=\frac{\sum f_{i} x_{i}^{2}}{n}-\left(\frac{\sum f_{i} x_{i}}{n}\right)^{2}$

Substituting values from above table and also given variance $=160$, we get

$160=\frac{92 \mathrm{~A}^{2}}{7}-\left(\frac{22 \mathrm{~A}}{7}\right)^{2}$

$160=\frac{92 \mathrm{~A}^{2}}{7}-\frac{484 \mathrm{~A}^{2}}{49}$

$160=\frac{7 \times 92 \mathrm{~A}^{2}-484 \mathrm{~A}^{2}}{49}$

$160=\frac{644 A^{2}-484 A^{2}}{49}$

$160=\frac{160 \mathrm{~A}^{2}}{49}$

$\Rightarrow \mathrm{A}^{2}=49$

$\Rightarrow \mathrm{A}=7$

Hence the value of $A$ is 7 .