The function

Download now India's Best Exam Prepration App Class 8-9-10, JEE & NEET
Video Lectures	Live Sessions
Study Material	Tests
Previous Year Paper	Revision

Video Lectures

Live Sessions

Study Material

Tests

Previous Year Paper

Revision

Question:
The function $f(x)=\left\{\begin{array}{l}\frac{\pi}{4}+\tan ^{-1} x,|x| \leq 1 \\ \frac{1}{2}(|x|-1),|x|>1\end{array}\right.$ is :

(1) continuous on $\mathbf{R}-\{1\}$ and differentiable on $\mathbf{R}-\{-1,1\} .$
(2) both continuous and differentiable on $\mathbf{R}-\{1\}$.
(3) continuous on $\mathbf{R}-\{-1\}$ and differentiable on $\mathbf{R}-\{-1,1\} .$
(4) both continuous and differentiable on $\mathbf{R}-\{-1\}$.

Correct Option: 1

Solution:

$f(x)= \begin{cases}\frac{-x-1}{2}, & x<-1 \\ \frac{\pi}{4}+\tan ^{-1} x, & -1 \leq x \leq 1 \\ \frac{1}{2}(x-1), & x>1\end{cases}$

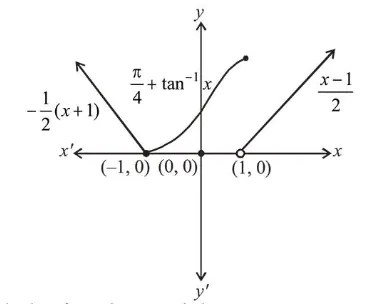
It is clear from above graph that, $f(x)$ is discontinuous at $x=1$.

i.e. continuous on $R-\{1\}$

$f(x)$ is non-differentiable at $x=-1,1$

i.e. differentiable on $R-\{-1,1\}$.