Question:
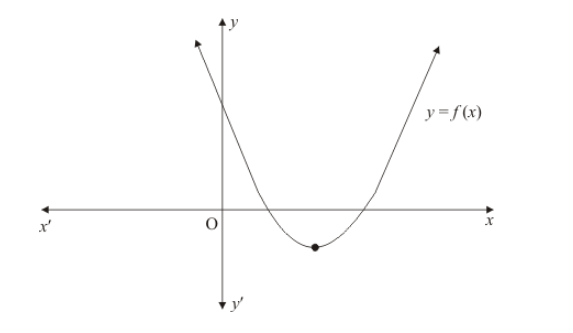
The graph of the polynomial $f(x)=a x^{2}+b x+c$ is as shown below (Fig. 2.19). Write the signs of 'a' and $b^{2}-4 a c$.
Solution:
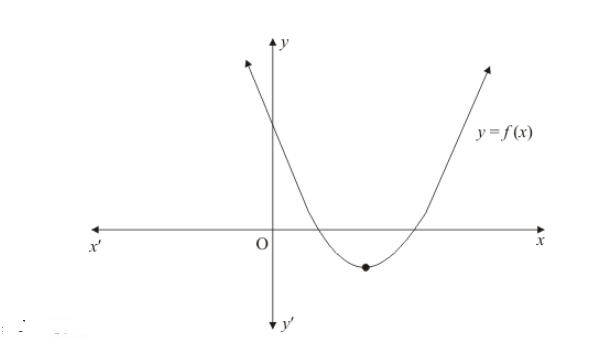
Clearly, $f(x)=a x^{2}+b x+c$ represent a parabola opening upwards. Therefore, $a>0$
Since the parabola cuts x-axis at two points, this means that the polynomial will have two real solutions
Hence $b^{2}-4 a c>0$
Hence $a>0$ and $b^{2}-4 a c>0$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
