The inside perimeter of a running track shown in the figure is 400 m. The length of each of the straight portions is 90 m, and the ends are semicircles. If the track is 14 m wide everywhere, find the area of the track. Also, find the length of the outer boundary of the track.
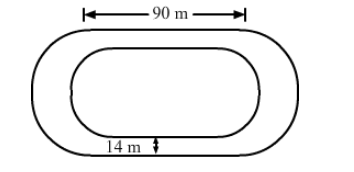
Lenath of the inner curved portion $(400-2 \times 90)=220 \mathrm{~m}$
$\therefore$ Length of each inner curved path $=\frac{220}{2}=110 \mathrm{~m}$
Thus, we have:
$\Rightarrow \pi \mathrm{r}=110$
$\Rightarrow \frac{22}{7} \mathrm{r}=110$
$\Rightarrow r=\frac{110 \times 7}{22}$
$\Rightarrow r=35 \mathrm{~m}$
Inner radius = 35 m
Outer radius = (35 + 14) = 49 m
Area of track $=\{$ Area of the two rectangles [each $(90 \times 14) \mathrm{m}]+$ Area of the circular ring with $\mathrm{R}=49 \mathrm{~m}$ and $\mathrm{r}=35 \mathrm{~m})\}$
$=(2 \times 90 \times 14)+\frac{22}{7} \times\left[(49)^{2}-(35)^{2}\right]$
$=2520+\frac{22}{7} \times(2401-1225)$
$=2520+\frac{22}{7} \times 1176$
$=2520+3696$
$=6216 \mathrm{~m}^{2}$
Length of the outer boundary of the track
$=\left(2 \times 90+2 \times \frac{22}{7} \times 49\right)$
$=488 \mathrm{~m}$
Therefore, the length of the outer boundary of the track is 488 m and the area of the track is 6216 sq. m.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
