The ionization constant of acetic acid is 1.74 × 10–5. Calculate the degree of dissociation of acetic acid in its 0.05 M solution.

Method 1

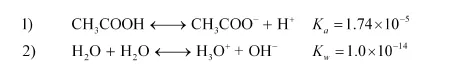
Since $K a>K_{w}:$

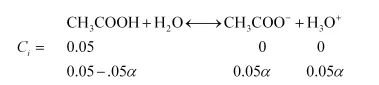
$K_{a}=\frac{(.05 \alpha)(.05 \alpha)}{(.05-0.05 \alpha)}$

$=\frac{(.05 \alpha)(0.05 \alpha)}{.05(1-\alpha)}$

$=\frac{.05 \alpha^{2}}{1-\alpha}$

$1.74 \times 10^{-5}=\frac{0.05 \alpha^{2}}{1-\alpha}$

$1.74 \times 10^{-5}-1.74 \times 10^{-5} \alpha=0.05 \alpha^{2}$

$0.05 \alpha^{2}+1.74 \times 10^{-5} \alpha-1.74 \times 10^{-5}$

$D=b^{2}-4 a c$

$=\left(1.74 \times 10^{-5}\right)^{2}-4(.05)\left(1.74 \times 10^{-5}\right)$

$=3.02 \times 10^{-25}+.348 \times 10^{-5}$

$\alpha=\sqrt{\frac{K_{a}}{c}}$

$\alpha=\sqrt{\frac{1.74 \times 10^{-5}}{.05}}$

$=\sqrt{\frac{34.8 \times 10^{-5} \times 10}{10}}$

$=\sqrt{3.48 \times 10^{-6}}$

$=\mathrm{CH}_{3} \mathrm{COOH} \longleftrightarrow \mathrm{CH}_{3} \mathrm{COO}^{-}+\mathrm{H}^{+}$

$\alpha \underline{1.86 \times 10^{-3}}$

$\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]=0.05 \times 1.86 \times 10^{-3}$

$=\frac{0.93 \times 10^{-3}}{1000}$

$=.000093$

Method 2

Degree of dissociation,

$\alpha=\sqrt{\frac{K_{a}}{c}}$

$c=0.05 \mathrm{M}$

$K_{a}=1.74 \times 10^{-5}$

Then, $\alpha=\sqrt{\frac{1.74 \times 10^{-5}}{.05}}$

$\alpha=\sqrt{34.8 \times 10^{-5}}$

$\alpha=\sqrt{3.48} \times 10^{-4}$

$\alpha=1.8610^{-2}$

$\mathrm{CH}_{3} \mathrm{COOH} \longleftrightarrow \mathrm{CH}_{3} \mathrm{COO}^{-}+\mathrm{H}^{+}$

Thus, concentration of $\mathrm{CH}_{3} \mathrm{COO}-=c . \alpha$

$=.05 \times 1.86 \times 10^{-2}$

$=.093 \times 10^{-2}$

$=.00093 \mathrm{M}$

Since $\left[\mathrm{oAc}^{-}\right]=\left[\mathrm{H}^{+}\right]$,

$\left[\mathrm{H}^{+}\right]=.00093=.093 \times 10^{-2}$

$\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]$

$=-\log \left(.093 \times 10^{-2}\right)$

$\therefore \mathrm{pH}=3.03$

Hence, the concentration of acetate ion in the solution is $0.00093 \mathrm{M}$ and its $\mathrm{Ph}$ is $3.03 .$