The length of a string between a kite and a point on the ground is 90 metres.

Let  be the kite of height m and the length of string between kite and a point on the ground is meters. Someters and

Now we have to find the height of kite.

We have the corresponding figure as follows

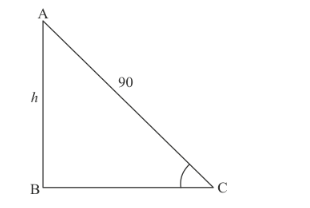
Given that $\tan \theta=\frac{15}{8}$

Since $\sec ^{2} \theta=1+\tan ^{2} \theta$

$\Rightarrow \quad \sec ^{2} \theta=1+\frac{225}{64}$

$\Rightarrow \quad \sec ^{2} \theta=\frac{289}{64}$

$\Rightarrow \quad \cos ^{2} \theta=\frac{64}{289}$

$\Rightarrow \quad \cos \theta=\frac{8}{17}$

Again,

Since $\sin ^{2} \theta=1-\cos ^{2} \theta$

$\Rightarrow \quad \sin ^{2} \theta=1-\frac{64}{289}$

$\Rightarrow \quad \sin ^{2} \theta=\frac{289-64}{289}$

$\Rightarrow \quad \sin \theta=\frac{15}{17}$

Now, in a triangle

$\Rightarrow \quad \sin \theta=\frac{h}{90}$

$\Rightarrow \quad \frac{15}{17}=\frac{h}{90}$

$\Rightarrow \quad h=\frac{15 \times 90}{17}$

$\Rightarrow \quad h=79.41$

Hence the height kite is $79.41$ meters.