The length of the minute hand of a clock is 14 cm.

We know that in 1 hour (i.e., 60 minutes), the minute hand rotates 360°.

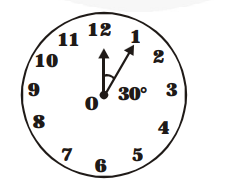
In 5 minutes, minute hand will rotate

$=\frac{\mathbf{3 6 0}^{\circ}}{\mathbf{6 0}} \times 5=30^{\circ}$

Therefore, the area swept by the minute hand in 5 minutes will be the area of a sector of 30° in a circle of 14 cm radius.

Area of sector of angle $\theta=\frac{\theta}{\mathbf{3 6 0}^{\circ}} \times \pi \mathrm{r}^{2}$

Area of sector of $30^{\circ}=\frac{\mathbf{3 0}^{\circ}}{\mathbf{3 6 0}^{\circ}} \times \frac{22}{\mathbf{7}} \times 14 \times 14$

$=\frac{22}{12} \times 2 \times 14=\frac{11 \times 14}{3}=\frac{154}{3} \mathrm{~cm}^{2}$

Therefore, the area swept by the minute hand in 5 minutes is $\frac{\mathbf{1 5 4}}{\mathbf{3}} \mathrm{cm}^{2}$