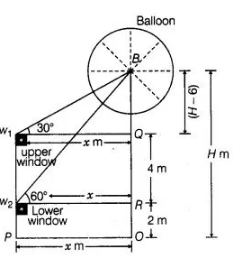
The lower window of a house is at a height of 2 m

Let the height of the balloon from above the ground is H.

A and OP=w2R=w1Q=x

Given that, height of lower window from above the ground = w2P = 2 m = OR

Height of upper window from above the lower window = w1w2 = 4 m = QR

$\therefore \quad B Q=O B-(Q R+R O)$

$=H-(4+2)$

$=H-6$

and $\quad \angle B w_{1} Q=30^{\circ}$

$\Rightarrow \quad \angle B W_{2} R=60^{\circ}$

Now, in $\triangle B w_{2} R$,

$\Rightarrow$ $\sqrt{3}=\frac{(H-6)+4}{x}$

$\Rightarrow$ $x=\frac{H-2}{\sqrt{3}}$ $\ldots(i)$

and in $\triangle B w, Q$, 

$\tan 30^{\circ}=\frac{B Q}{w_{1} Q}$

$\tan 30^{\circ}=\frac{H-6}{x}=\frac{1}{\sqrt{3}}$

$\Rightarrow \quad x=\sqrt{3}(H-6) \quad \ldots$ (ii)

From Eqs. (i) and (ii),

$\sqrt{3}(H-6)=\frac{(H-2)}{\sqrt{3}}$

$3(H-6)=H-2=3 H-18=H-2$

$\Rightarrow \quad 2 H=16 \Rightarrow H=8$

So, the required height is 8 m.

Hence, the required height of the ballon’from above the ground is 8 m.