Question:
The masses and radii of the earth and moon are $\left(\mathrm{M}_{1}, \mathrm{R}_{1}\right)$ and $\left(\mathrm{M}_{2}, \mathrm{R}_{2}\right)$ respectively. Their centres are at a distance ' $r$ ' apart. Find the minimum escape velocity for a particle of mass ' $m$ ' to be projected from the middle of these two masses:
Correct Option: , 2
Solution:
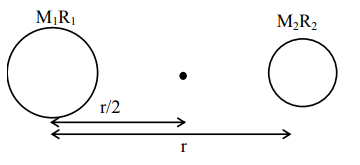
$\frac{1}{2} \mathrm{mV}^{2}-\frac{\mathrm{GM}_{1} \mathrm{~m}}{\mathrm{r} / 2}-\frac{\mathrm{GM}_{2} \mathrm{~m}}{\mathrm{r} / 2}=0$
$\frac{1}{2} \mathrm{mV}^{2}=\frac{2 \mathrm{Gm}}{\mathrm{r}}\left(\mathrm{M}_{1}+\mathrm{M}_{2}\right)$
$V=\sqrt{\frac{4 G\left(M_{1}+M_{2}\right)}{r}}$
Option (2)