The maximum volume (in cu.m) of the right circular cone having slant height

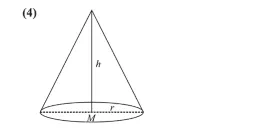
$h^{2}+r^{2}=\ell^{2}=9$ ........(1)

Volume of cone

$V=\frac{1}{3} \pi r^{2} h$ ..........(2)

From (1) and (2),

$\Rightarrow \quad V=\frac{1}{3} \pi\left(9-h^{2}\right) h$

$\Rightarrow \quad V=\frac{1}{3} \pi\left(9 h-h^{3}\right)$  $\Rightarrow \frac{d v}{d h}=\frac{1}{3} \pi\left(9-3 h^{2}\right)$

For maxima/minima,

$\frac{d V}{d h}=0 \Rightarrow \frac{1}{3} \pi\left(9-3 h^{2}\right)=0$

$\Rightarrow h=\pm \sqrt{3} \Rightarrow h=\sqrt{3}$ $(\because h>0)$

Now; $\frac{d^{2} V}{d h^{2}}=\frac{1}{3} \pi(-6 h)$

Here, $\left(\frac{d^{2} V}{d h^{2}}\right)_{\text {at } h=\sqrt{3}}<0$

Then, $h=\sqrt{3}$ is point of maxima

Hence, the required maximum volume is,

$V=\frac{1}{3} \pi(9-3) \sqrt{3}=2 \sqrt{3} \pi$