Question:
The mean of the following distribution is 50.
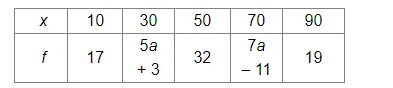
Find the value of a and hence the frequencies of 30 and 70.
Solution:
We know that,
Mean $=\frac{\sum x_{i} f_{i}}{\sum f_{i}}$
For the following data:
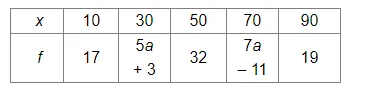
Mean $=\frac{(10 \times 17)+(30 \times(5 a+3))+(50 \times 32)+(70 \times(7 a-11))+(90 \times 19)}{17+5 a+3+32+7 a-11+19}$
$\Rightarrow 50=\frac{170+150 a+90+1600+490 a-770+1710}{60+12 a}$
$\Rightarrow 50(60+12 a)=2800+640 a$
$\Rightarrow 3000+600 a=2800+640 a$
$\Rightarrow 640 a-600 a=3000-2800$
$\Rightarrow 40 a=200$
$\Rightarrow a=\frac{200}{40}$
$\Rightarrow a=5$
Hence, the value of a is 5.
Also, the frequency of 30 is 28 and the frequency of 70 is 24.
