The mean of the following frequency distribution

First we caluculate the class mark of given data

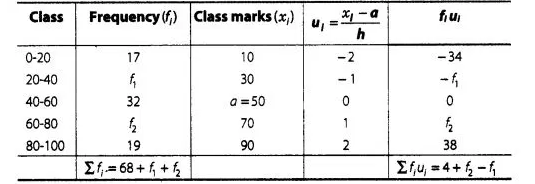
Given that, sum of all frequencies $=120$

$\Rightarrow \quad \Sigma f_{1}=68+f_{1}+f_{2}=120$

$\Rightarrow \quad f_{1}+f_{2}=52$ $\ldots(\mathrm{i})$

Here, $\quad$ (assumed mean) $a=50$

and (class width) $h=20$

By step deviation method,

Mean $=a+\frac{\Sigma f_{i} u_{l}}{\Sigma f_{j}} \times h$

$\Rightarrow$ $50=50+\frac{\left(4+t_{2}-f_{12}\right.}{120} \times 20$

$\Rightarrow \quad 4+t_{2}-t_{1}=0$

$\Rightarrow \quad-f_{2}+f_{1}=4$ ...(ii)

On adding Eqs. (i) and (ii), we get

$2 f_{1}=56$

$\Rightarrow \quad f_{1}=28$

Put the value of $f_{1}$ in Eq. (i), we get

$f_{2}=52-28$

$\Rightarrow \quad f_{2}=24$

Hence, $f_{1}=28$ and $f_{2}=24$