The median BE and CF of a triangle ABC

Given In $\triangle A B C$, medians $B E$ and $C F$ intersect each other at $G$.

To prove To prove $\operatorname{ar}(\Delta G B C)=\operatorname{ar}(A F G E)$

Proof Since, $B E$ is the median of $\triangle A B C$ and we know that a median of a triangle divides it into two parts of equal area.

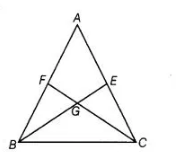
So, $\quad$ ar $(\Delta A B E)=\operatorname{ar}(\Delta C B E)$

$\Rightarrow \quad \operatorname{ar}(\Delta A B E)=\frac{1}{2} \operatorname{ar}(\triangle A B C)$ $\ldots($ i)

Similarly, $C F$ is the median of $\triangle A B C$.

Then, $\operatorname{ar}(\Delta A C F)=\operatorname{ar}(\Delta B C F)$

$\Rightarrow$ $\operatorname{ar}(\Delta B C F)=\frac{1}{2} \operatorname{ar}(\triangle A B C)$ .....(ii)

From Eqs. (i) and (ii),

$\operatorname{ar}(\triangle A B E)=\operatorname{ar}(\triangle B C F)$ $\ldots$ (iii)

On subtracting ar ( $\Delta G B F$ ) from both sides of Eq. (iii), we get

$\operatorname{ar}(\Delta A B E)-\operatorname{ar}(\Delta G B F)=\operatorname{ar}(\Delta B C F)-\operatorname{ar}(\Delta G B F)$

$\Rightarrow$ $\operatorname{ar}(A F G E)=\operatorname{ar}(G B C)$ 

Hence proved.