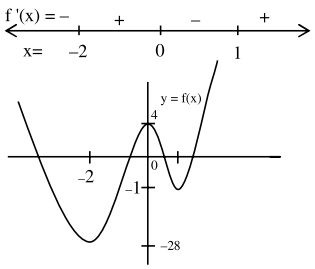
Question:
The number of distinct real roots of the equation $3 x^{4}+4 x^{3}-12 x^{2}+4=0$ is
Solution:
$3 x^{4}+4 x^{3}-12 x^{2}+4=0$
So, Let $f(x)=3 x^{4}+4 x^{3}-12 x^{2}+4$
$\therefore \mathrm{f}^{\prime}(\mathrm{x})=12 \mathrm{x}\left(\mathrm{x}^{2}+\mathrm{x}-2\right)$
$=12 x(x+2)(x-1)$