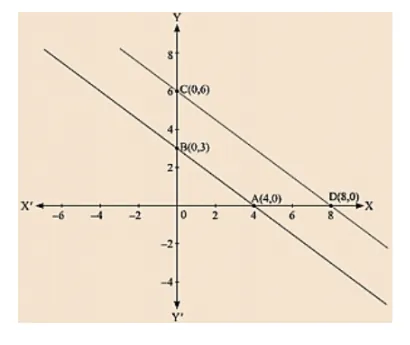
The path of a train A is given by the equation 3x + 4y -12 = 0

We are given the path of train A, 3x + 4y - 12 = 0

We get, 

$y=\frac{12-3 x}{4}$

Now, substituting x = 0 in

$y=\frac{12-3 x}{4}$

we get y = 3

Substituting x = 4 in

$y=\frac{12-3 x}{4}$

we get y = 0

Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

Plotting A(4, 0) and E(0, 3) on the graph and by joining the points,

we obtain the graph of equation 3x + 4y - 12 = 0.

We are given the path of train B, 6x + 8y - 48 = 0

We get,

$y=\frac{48-6 x}{8}$

Now, substituting x = 0 in

$y=\frac{48-6 x}{8}$

we get y = 6

Substituting x = 8 in

$y=\frac{48-6 x}{8}$

we get y = 0

Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation 

Plotting C (0, 6) and D (8, 0) on the graph and by joining the points. We obtain the graph of equation 6x + 8y – 48 = 0