The perimeter of a triangle with vertices (0, 4),

(b) we Further, adding all the distance of a triangle to get the perimeter of a triangle.We plot the vertices of a triangle i.e., (0, 4), (0,0) and (3,0) on

the paper shown as given below

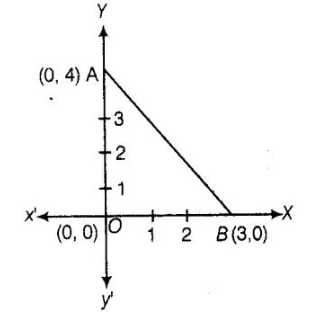
Now,perimeter of ΔAOB=Sum of the length of all its sides = d(AO) + d(OB) + d(AB)

∴ Distance between the points (x1,y1) and (x2, y2),

$d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}$

$=$ Distance between $A(0,4)$ and $O(0,0)+$ Distance between $O(0,0)$ and $B(3,0)$

+ Distance between $A(0,4)$ and $B(3,0)$

$=\sqrt{(0-0)^{2}+(0-4)^{2}}+\sqrt{(3-0)^{2}+(0-0)^{2}}+\sqrt{(3-0)^{2}+(0-4)^{2}}$

$=\sqrt{0+16}+\sqrt{9+0}+\sqrt{(3)^{2}+(4)^{2}}=4+3+\sqrt{9+16}$

$=7+\sqrt{25}=7+5=12$

Hence, the required perimeter of triangle is 12.