The perpendicular bisector of the line segment

(a) Firstly, we plot the points of the line segment on the paper and join them.

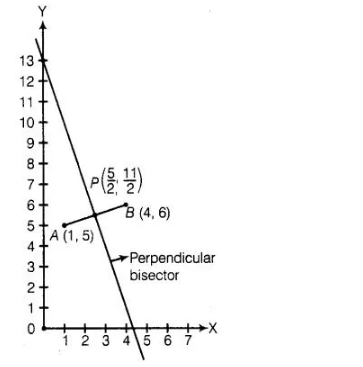
We know that, the perpendicular bisector of the line segment AB bisect the segment AB, i.e., perpendicular bisector of line segment AB passes

through the mid-point of AB.

$\therefore \quad$ Mid-point of $A B=\left(\frac{1+4}{2}, \frac{5+6}{2}\right)$

$\Rightarrow \quad P=\left(\frac{5}{2}, \frac{11}{2}\right)$

$\left[\because\right.$ mid-point of line segment passes through the points $\left(x_{1}, y_{1}\right)$ and $\left(x_{2}, y_{2}\right)$$\left.=\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\right]$

Now, we draw a straight line on paper passes through the mid-point P. We see that the perpendicular bisector cuts the Y-axis at the point (0,13).

Hence, the required point is (0,13).

Alternate Method

We know that, the equation of line which passes through the points (x1, y1) and (x2, y2) is

$\left(y-y_{1}\right)=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\left(x-x_{1}\right)$ $\ldots$ (i)

Here, $x_{1}=1, y_{1}=5$ and $x_{2}=4, y_{2}=6$

So, the equation of line segment joining the points $A(1,5)$ and $B(4,6)$ is

$(y-5)=\frac{6-5}{4-1}(x-1)$

$\Rightarrow$ $(y-5)=\frac{1}{3}(x-1)$

$\Rightarrow$ $3 y-15=x-1$

$\Rightarrow$ $3 y=x-14 \Rightarrow y=\frac{1}{3} x-\frac{14}{3}$ .....(ii)

$\therefore$ Slope of the line segment, $m_{1}=\frac{1}{3}$

If two lines are perpendicular to each other, then the relation between its slopes is

$m_{1} \cdot m_{2}=-1$ ...(iii)

where, $\quad m_{1}=$ Slope of line 1

and $\quad=$ Slope of line 2

Also, we know that the perpendicular bisector of the line segment is perpendicular on the line segment.

Let slope of line segment is m2.

From Eq. (iii),

$m_{1} \cdot m_{2}=\frac{1}{3} \cdot m_{2}=-1$

$\Rightarrow \quad m_{2}=-3$

Also we know that the perpendicular bisector is passes through the mid-point of line segment.

$\therefore \quad$ Mid-point of line segment $=\left(\frac{1+4}{2}, \frac{5+6}{2}\right)=\left(\frac{5}{2}, \frac{11}{2}\right)$

Equation of perpendicular bisector, which has slope $(-3)$ and passes through the point

$\left(\frac{5}{2}, \frac{11}{2}\right), 15$

$\left(y-\frac{11}{2}\right)=(-3)\left(x-\frac{5}{2}\right)$

[since, equation of line passes through the point $\left(x_{1}, y_{1}\right)$ and having slope $m$ $\left.\left(y-y_{1}\right)=m\left(x-x_{1}\right)\right]$

$\Rightarrow \quad(2 y-11)=-3(2 x-5)$

$\Rightarrow \quad 2 y-11=-6 x+15$

$\Rightarrow \quad 6 x+2 y=26$

$\Rightarrow \quad 3 x+y=13$ $\ldots(\mathrm{IV})$

If the perpendicular bisector cuts the $Y$-axis, then put $x=0$ in Eq. (iv),

$3 \times 0+y=13 \Rightarrow y=13$

So, the required point is (0,13).