The perpendicular from $A$ on side $B C$ of a $\triangle A B C$ intersects $B C$ at $D$ such that $D B=3 C D(s e e$ figure).
Question.
The perpendicular from $A$ on side $B C$ of a $\Delta A B C$ intersects $B C$ at $D$ such that $D B=3 C D(s e e$ figure). Prove that $2 \mathrm{AB}^{2}=2 \mathrm{AC}^{2}+\mathrm{BC}^{2}$.
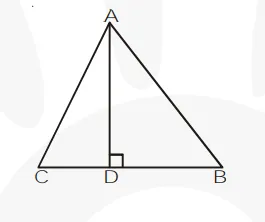
The perpendicular from $A$ on side $B C$ of a $\Delta A B C$ intersects $B C$ at $D$ such that $D B=3 C D(s e e$ figure). Prove that $2 \mathrm{AB}^{2}=2 \mathrm{AC}^{2}+\mathrm{BC}^{2}$.

Solution:
DB = 3 CD
$\Rightarrow \mathrm{CD}=\frac{1}{4} \mathrm{BC}$ ...(1)
and $D B=\frac{3}{4} B C$
In $\triangle \mathrm{ABD}, \quad \mathrm{AB}^{2}=\mathrm{DB}^{2}+\mathrm{AD}^{2}$
In $\Delta \mathrm{ACD}, \quad \mathrm{AC}^{2}=\mathrm{CD}^{2}+\mathrm{AD}^{2}$
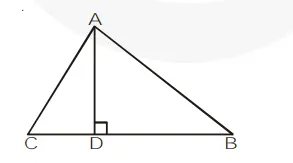
Subtracting (3) from (2), we get
$\mathrm{AB}^{2}-\mathrm{AC}^{2}=\mathrm{DB}^{2}-\mathrm{CD}^{2}$
$=\left(\frac{3}{4} \mathrm{BC}\right)^{2}-\left(\frac{1}{4} \mathrm{BC}\right)^{2}=\frac{9}{16} \mathrm{BC}^{2}-\frac{1}{16} \mathrm{BC}^{2}$
$=\frac{1}{2} \mathrm{BC}^{2} \Rightarrow 2 \mathrm{AB}^{2}-2 \mathrm{AC}^{2}=\mathrm{BC}^{2}$
$\Rightarrow 2 \mathrm{AB}^{2}=2 \mathrm{AC}^{2}+\mathrm{BC}^{2}$
Hence proved.
DB = 3 CD
$\Rightarrow \mathrm{CD}=\frac{1}{4} \mathrm{BC}$ ...(1)
and $D B=\frac{3}{4} B C$
In $\triangle \mathrm{ABD}, \quad \mathrm{AB}^{2}=\mathrm{DB}^{2}+\mathrm{AD}^{2}$
In $\Delta \mathrm{ACD}, \quad \mathrm{AC}^{2}=\mathrm{CD}^{2}+\mathrm{AD}^{2}$

Subtracting (3) from (2), we get
$\mathrm{AB}^{2}-\mathrm{AC}^{2}=\mathrm{DB}^{2}-\mathrm{CD}^{2}$
$=\left(\frac{3}{4} \mathrm{BC}\right)^{2}-\left(\frac{1}{4} \mathrm{BC}\right)^{2}=\frac{9}{16} \mathrm{BC}^{2}-\frac{1}{16} \mathrm{BC}^{2}$
$=\frac{1}{2} \mathrm{BC}^{2} \Rightarrow 2 \mathrm{AB}^{2}-2 \mathrm{AC}^{2}=\mathrm{BC}^{2}$
$\Rightarrow 2 \mathrm{AB}^{2}=2 \mathrm{AC}^{2}+\mathrm{BC}^{2}$
Hence proved.
