The points A(x1, y1), B(x2 y2) and C(x3, y3) are the vertices of ΔABC.
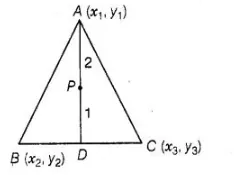
(i) The median from A meets BC at Find the coordinates of the point D.
(ii) Find the coordinates of the point P on AD such that AP : PD = 2:1
(iii) Find the coordinates of points Q and R on medians BE and CF, respectively such that BQ:QE = 2:1 and CR:RF = 2:1
(iv ) What are the coordinates of the centroid of the ΔABC?
Given that, the points A (x1, y1), B(x2, y2)andC (x3, y3)are the vertices of ΔABC.
(i) We know that, the median bisect the line segment into two equal parts i.e., here D is the mid-point of BC.
$\therefore$ Coordinate of mid-point of $B C=\left(\frac{x_{2}+x_{3}}{2}, \frac{y_{2}+y_{3}}{2}\right)$
$\Rightarrow$ $D \equiv\left(\frac{x_{2}+x_{3}}{2}, \frac{y_{2}+y_{3}}{2}\right)$
(ii) Let the coordinates of a point $P$ be $(x, y)$.
Given that, the point $P(x, y)$, divide the line joining $A\left(x_{1}, y_{1}\right)$ and $D\left(\frac{x_{2}+x_{3}}{2}, \frac{y_{2}+y_{3}}{2}\right)$ in
the ratio $2: 1$, then the coordinates of $P$
$=\left[\frac{2 \cdot\left(\frac{x_{2}+x_{3}}{2}\right)+1 \cdot x_{1}}{2+1}, \frac{2 \cdot\left(\frac{y_{2}+y_{3}}{2}\right)+1 \cdot y_{1}}{2+1}\right]$
$\left[\because\right.$ internal section formula $\left.=\left(\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}, \frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}\right)\right]$
$\equiv\left(\frac{x_{2}+x_{3}+x_{1}}{3}, \frac{y_{2}+y_{3}+y_{1}}{2}\right)$
$\therefore$ So, required coordinates of point $P \equiv\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)$
(iii) Let the coordinates of a point $Q$ be $(p, q)$
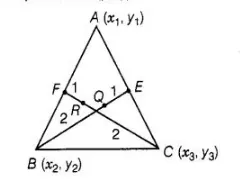
Given that, the point $Q(p, q)$, divide the line joining $B\left(x_{2}, y_{2}\right)$ and $E\left(\frac{x_{1}+x_{3}}{2}, \frac{y_{1}+y_{3}}{2}\right)$ in
the ratio $2: 1$, then the coordinates of $Q$
$\equiv\left[\frac{2 \cdot\left(\frac{x_{1}+x_{3}}{2}\right)+1 \cdot x_{2}}{2+1}, \frac{2 \cdot\left(\frac{y_{1}+y_{2}}{2}\right)+1 \cdot y_{2}}{2+1}\right]$
$=\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)$
$[$ since, $B E$ is the median of side $C A$, so $B E$ divides $A C$ in to two equal parts.
$\therefore$ mid-point of $A C=$ Coordinate of $\left.E \Rightarrow E=\left(\frac{x_{1}+x_{3}}{2}, \frac{y_{1}+y_{3}}{2}\right)\right]$
So, the required coordinate of point $Q \equiv\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)$
Now, let the coordinates of a point $E$ be $(\alpha, \beta)$. Given that, the point $R(\alpha, \beta)$, divide the line
joining $C\left(x_{3}, y_{3}\right)$ and $F\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)$ in the ratio $2: 1$, then the coordinates of $R$
$\equiv\left[\frac{2 \cdot\left(\frac{x_{1}+x_{2}}{2}\right)+1 \cdot x_{3}}{2+1}, \frac{2 \cdot\left(\frac{y_{1}+y_{2}}{2}\right)+1 \cdot y_{3}}{2+1}\right]$
$=\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)$
[ since, $C F$ is the median of side $A B$. So, $C F$ divides $A B$ in to two equal parts.
$\therefore$ mid-point of $A B=$ coordinate of $\left.F \Rightarrow F=\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\right]$
So, the required coordinate of point $R \equiv\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)$
(iv) Coordinate of the centroid of the $\triangle A B C$
$=\left(\frac{\text { Sum of abscissa of all vertices }}{3}, \frac{\text { Sum of ordinate of all vertices }}{3}\right)$
$=\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)$
