The probability distribution of random variable $\mathrm{X}$ is given by:
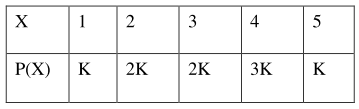
Let $\mathrm{p}=\mathrm{P}(1<\mathrm{X}<4 \mid \mathrm{X}<3) .$ If $5 \mathrm{p}=\lambda \mathrm{K}$, then $\lambda$ equal to
$\sum \mathrm{P}(\mathrm{X})=1 \Rightarrow \mathrm{k}+2 \mathrm{k}+2 \mathrm{k}+3 \mathrm{k}+\mathrm{k}=1$
$\Rightarrow \mathrm{k}=\frac{1}{9}$
Now, $\mathrm{p}=\mathrm{P}\left(\frac{\mathrm{k} \mathrm{X}<4}{\mathrm{X}<3}\right)=\frac{\mathrm{P}(\mathrm{X}=2)}{\mathrm{P}(\mathrm{X}<3)}=\frac{\frac{2 \mathrm{k}}{9 \mathrm{k}}}{\frac{\mathrm{k}}{9 \mathrm{k}}+\frac{2 \mathrm{k}}{9 \mathrm{k}}}=\frac{2}{3}$
$\Rightarrow \mathrm{p}=\frac{2}{3}$
Now, $5 \mathrm{p}=\lambda \mathrm{k}$
$\Rightarrow(5)\left(\frac{2}{3}\right)=\lambda(1 / 9)$
$\Rightarrow \lambda=30$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
