The quadrilateral formed by joining the

(d) Given, the quadrilateral $A B C D$ is a rhombus. So, sides $A B, B C, C D$ and $A D$ are equal.

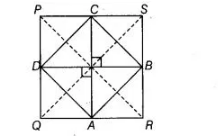
Now, in $\triangle P Q S$, we have

$D$ and $C$ are the mid-points of $P Q$ and $P S$.

So, $\quad D C=\frac{1}{2} Q S$  [by mid-point theorem] ...(i)

Similarly, in $\triangle P S R$

$B C=\frac{1}{2} P R$   [by mid-point theorem] ...(ii)

As $\quad B C=D C \quad$ [since, $A B C D$ is a rhombus]

$\therefore \quad \frac{1}{2} Q S=\frac{1}{2} P R \quad$ [from Eqs. (i) and (ii)]

$\Rightarrow \quad Q S=P R$

Hence, diagonals of $P Q R S$ are equal.