The radii of two cylinders are in the ratio 3 : 5

Given that, $r_{1}: r_{2}=3: 5$ and $h_{1}: h_{2}=2: 3$

Now, the ratio of their curved surface area $s_{1}: s_{2}=2 \pi r_{1} h_{1}: 2 \pi r_{2} h_{2}$

$s_{1}: s_{2}=2 \pi r_{1} h_{1}: 2 \pi r_{2} h_{2}$

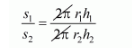
$=\left(\frac{r_{1}}{r_{2}}\right)\left(\frac{h_{1}}{h_{2}}\right)$

$\frac{s_{1}}{s_{2}}=\frac{3}{5} \times \frac{2}{3}=\frac{2}{5}$

Hence, $s_{1}: s_{2}=2: 5$