The rate constant for the decomposition of N2O5 at various temperatures is given below:
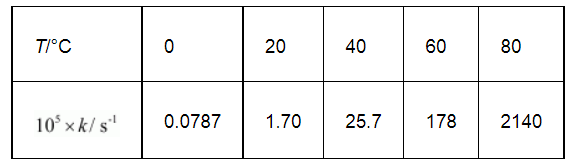
Draw a graph between ln k and 1/T and calculate the values of A and Ea.
Predict the rate constant at 30º and 50ºC.
From the given data, we obtain
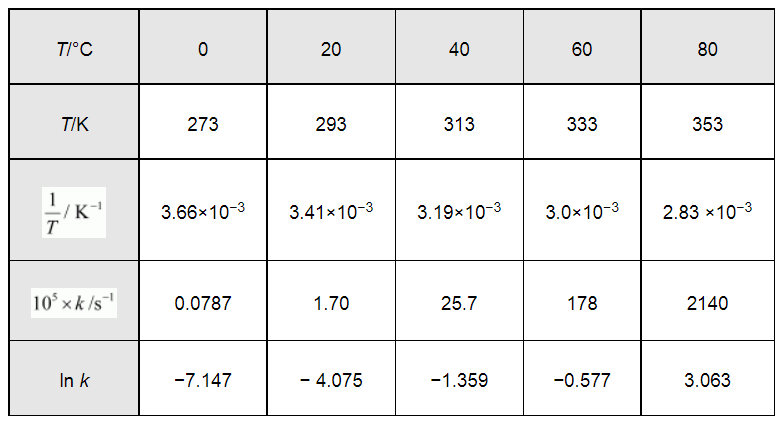
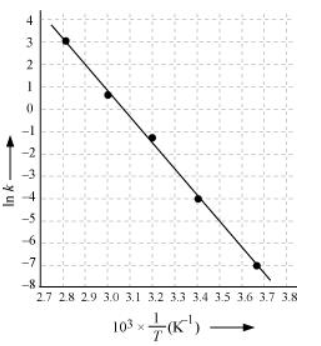
Slope of the line,
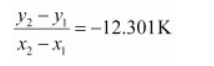
According to Arrhenius equation,
Slope $=-\frac{E_{a}}{R}$
$\Rightarrow E_{a}=-S$ lope $\times \mathrm{R}$
$=-(-12.301 \mathrm{~K}) \times\left(8.314 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\right)$
$=102.27 \mathrm{~kJ} \mathrm{~mol}^{-1}$
Again,
$\ln k=\ln A-\frac{E_{a}}{\mathrm{R} T}$
$\ln A=\ln k+\frac{E_{a}}{\mathrm{R} T}$
When $T=273 \mathrm{~K}$,
$\ln k=-7.147$
Then, $\ln A=-7.147+\frac{102.27 \times 10^{3}}{8.314 \times 273}$
$=37.911$
Therefore, $A=2.91 \times 10^{6}$
When $T=30+273 \mathrm{~K}=303 \mathrm{~K}$,
$\frac{1}{T}=0.0033 \mathrm{~K}=3.3 \times 10^{-3} \mathrm{~K}$
Then, at $\frac{1}{T}=3.3 \times 10^{-3} \mathrm{~K}$,
$\ln k=-2.8$
Therefore, $k=6.08 \times 10^{-2} \mathrm{~s}^{-1}$
Again, when $T=50+273 \mathrm{~K}=323 \mathrm{~K}$,
$\frac{1}{T}=0.0031 \mathrm{~K}=3.1 \times 10^{-3} \mathrm{~K}$
Then, at $\frac{1}{T}=3.1 \times 10^{-3} \mathrm{~K}$,
In $k=-0.5$
Therefore, $k=0.607 \mathrm{~s}^{-1}$
