The ratio of the outer and inner perimeters of a

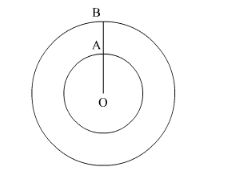
Let OA = r be the radius of the inner circle and OB = r′ be the radius of the outer circle.

Therefore, circumference of the inner circle $=2 \pi r$ and circumference of the outer circle $=2 \pi r^{\prime}$

Here we have to find the diameter of the inner circle.

We have given the ratio of outer and inner perimeters of a circular path.

$\therefore \frac{2 \pi r^{\prime}}{2 \pi r}=\frac{23}{22}$

Simplifying the above equation we get,

$\frac{r^{\prime}}{r}=\frac{23}{22}$

$\therefore 22 r^{\prime}=23 r$

$\therefore 22 r^{\prime}-23 r=0$....(1)

We have also given that the path is 5 meters wide, that is we have given

$r^{\prime}-r=5 \ldots \ldots .(2)$

We are asked to find the diameter of the inner circle hence, we will eliminate r′ using equations (1) and (2) for that we will multiply equation (2) by 22.

$22 r^{\prime}-22 r=110 \ldots \ldots \ldots(3)$

Subtracting equation (1) from equation (3) we get, $r=110$

Therefore, radius of the inner circle is 110 meters.

Therefore, diameter of the inner circle $=2 \times 110=220$ meters

Therefore, diameter of the inner circle is 220 meters.

Hence, the correct answer is option (c).