The shadow of a tower standing on a level ground is found to be 40 m

Let  be the tower of height.given the shadow of tower m. attitude of sun are  and. Here we have to find height of tower. Let  and .

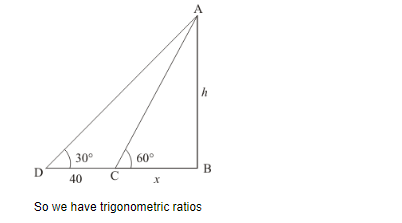
In $\triangle A C B$

$\Rightarrow \quad \tan C=\frac{A B}{B C}$

$\Rightarrow \quad \tan 60^{\circ}=\frac{h}{x}$

$\Rightarrow \quad \sqrt{3}=\frac{h}{x}$

$\Rightarrow \quad x=\frac{h}{\sqrt{3}}$

Again in $\triangle A D B$

$\Rightarrow \quad \tan D=\frac{A B}{D B}$

$\Rightarrow \quad \tan 30^{\circ}=\frac{h}{40+x}$

$\Rightarrow \quad \frac{1}{\sqrt{3}}=\frac{h}{40+x}$

$\Rightarrow \quad 40+x=\sqrt{3} h$

Put $x=\frac{h}{\sqrt{3}}$

$\Rightarrow \quad 40+\frac{h}{\sqrt{3}}=\sqrt{3} h$

$\Rightarrow \quad 40=\sqrt{3} h-\frac{h}{\sqrt{3}}$

$\Rightarrow \quad 40=\frac{2 h}{\sqrt{3}}$

$\Rightarrow \quad h=20 \sqrt{3}$

Hence height of tower is $20 \sqrt{3} \mathrm{~m}$.