Question:
The shortest distance between the line $x-y=1$ and the curve $x^{2}=2 y$ is :
Correct Option: , 2
Solution:
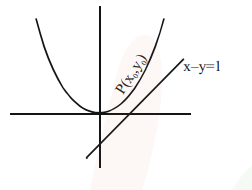
Shortest distance between curves is always along common normal.
$\left.\frac{d y}{d x}\right|_{P}=$ slope of line $=1$
$\Rightarrow x_{0}=1$ $\therefore \mathrm{y}_{0}=\frac{1}{2}$
$\Rightarrow \mathrm{P}\left(1, \frac{1}{2}\right)$
$\therefore$ Shortest distance $=\left|\frac{1-\frac{1}{2}-1}{\sqrt{1^{2}+1^{2}}}\right|=\frac{1}{2 \sqrt{2}}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
