The shortest distance between the point

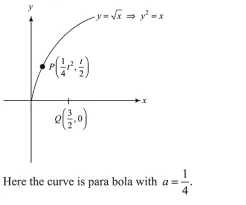
Here the curve is para bola with $a=\frac{1}{4}$,

Let $\mathrm{P}\left(\mathrm{at}^{2}\right.$, 2at) i.e., $P\left(\frac{t^{2}}{4}, \frac{t}{2}\right)$ be a point on the curve.

Now, $y^{2}=x$

$\Rightarrow 2 y \frac{d y}{d x}=1 \Rightarrow \frac{d y}{d x}=\frac{1}{2 \sqrt{x}}$

$\Rightarrow\left(\frac{d y}{d x}\right)_{a t p}=\frac{1}{t}$

$\therefore$ Equation of normal at $P$ to $y^{2}=x$ is,

$\left(y-\frac{t}{2}\right)=-t\left(x-\frac{1}{4} t^{2}\right)$

$\Rightarrow y=-t x+\frac{1}{2} t+\frac{1}{4} t^{3}$ .........(1)

For minimum $P Q,(1)$ passes through $Q\left(\frac{3}{2}, 0\right)$

$\Rightarrow \frac{-3}{2} t+\frac{t}{2}+\frac{t^{3}}{4}=0 \Rightarrow-4 t+t^{3}=0$

$\Rightarrow t\left(t^{2}-4\right)=0 \Rightarrow t=-2,0,2$

$\because t \geq 0 \Rightarrow t=0,2$

If $t=0, P(0,0) \Rightarrow A P=\frac{3}{2}$

If $t=2, P(1,1) \Rightarrow A P=\frac{\sqrt{5}}{2}$

$\Rightarrow$ Shortest distance $\left(\frac{3}{2}, 0\right)$ and $y=\sqrt{x}$ is $\frac{\sqrt{5}}{2}$