The slant height of a frustum of a cone is 4 cm and the perimeters (circumference) of its circular ends are 18 cm and 6 cm.

We have

Slant height $(\ell)=4 \mathrm{~cm}$ 

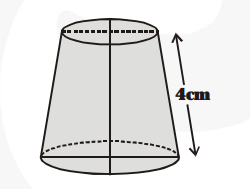
$2 \pi r_{1}=18 \mathrm{~cm}$ and $2 \pi r_{2}=6 \mathrm{~cm}$

$\Rightarrow \pi r_{1}=\frac{\mathbf{1 8}}{\mathbf{2}}=9 \mathrm{~cm}$ and $\pi r_{2}=\frac{\mathbf{6}}{\mathbf{2}}=3 \mathrm{~cm}$

$\therefore$ Curved surface area of the frustum of the cone

$=\pi\left(r_{1}+r_{2}\right) \ell=\left(\pi r_{1}+\pi r_{2}\right) \ell=(9+3) \times 4 \mathrm{~cm}^{2}$

$=12 \times 4 \mathrm{~cm}^{2}=48 \mathrm{~cm}^{2}$