The tangent at a point C of a circle

Here, AB is a diameter of the circle from point C and a tangent is drawn which meets at a point P.

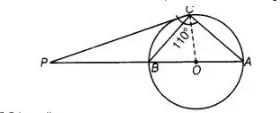
Join OC. Here, OC is radius.

Since, tangent at any point of a circle is perpendicular to the radius through point of contact circle.

$\therefore \quad O C \perp P C$

Now, $\angle P C A=110^{\circ}$ [given]

\$\Rightarrow \quad \angle P C O+\angle O C A=110^{\circ}$

$\Rightarrow \quad 90^{\circ}+\angle O C A=110^{\circ}$

$\Rightarrow \quad \angle O C A=20^{\circ}$

$\therefore$ $O C=O A=$ Radius of circle

$\Rightarrow$ $\angle O C A=\angle O A C=20^{\circ}$

[since, two sides are equal, then their opposite angles are equal]

Since, $P C$ is a tangent, so $\angle B C P=\angle C A B=20^{\circ}$ 

[angles in a alternate segment are equal]

In $\triangle P B C, \quad \angle P+\angle C+\angle A=180^{\circ}$

$\angle P=180^{\circ}-(\angle C+\angle A)$

$=180^{\circ}-\left(110^{\circ}+20^{\circ}\right)$

$=180^{\circ}-130^{\circ}=50^{\circ}$

in $\triangle P B C, \quad \angle B P C+\angle P C B+\angle P B C=180^{\circ}$ 

[sum of all interior angles of any triangle is $180^{\circ}$ ]

$\Rightarrow \quad 50^{\circ}+20^{\circ}+\angle P B C=180^{\circ}$

$\Rightarrow \quad \angle P B C=180^{\circ}-70^{\circ}$

$\Rightarrow \quad \angle P B C=110^{\circ}$

Since, $A P B$ is a straight line.

$\therefore \quad \angle P B C+\angle C B A=180^{\circ}$

$\Rightarrow \quad \angle C B A=180^{\circ}-110^{\circ}=70^{\circ}$