The top of a ladder 6 metres long is resting against a vertical wall on a level pavement, when the ladder begins to slide outwards. At the moment when the foot of the ladder is 4 metres from the wall, it is sliding away from the wall at the rate of 0.5 m/sec. How fast is the top-sliding downwards at this instance?
How far is the foot from the wall when it and the top are moving at the same rate?
Let the bottom of the ladder be at a distance of x m from the wall and its top be at a height of y m from the ground.
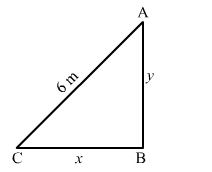
Here,
$x^{2}+y^{2}=36$
$\Rightarrow 2 x \frac{d x}{d t}=-2 y \frac{d y}{d t}$ .....(1)
When $x=4, y=\sqrt{36-16}=2 \sqrt{5}$
$\Rightarrow 2 \times 4 \times 0.5=-2 \times 2 \sqrt{5} \frac{d y}{d t}$ $\left[\because \frac{d x}{d t}=0.5 \mathrm{~m} / \mathrm{sec}\right]$
$\Rightarrow \frac{d y}{d t}=\frac{-1}{\sqrt{5}} \mathrm{~m} / \mathrm{sec}$
From eq. $(1)$, we get
$2 x \frac{d x}{d t}=-2 y \frac{d y}{d t}$ $\left[\because \frac{d x}{d t}=\frac{d y}{d t}\right]$
$\Rightarrow x=-y$
Substituting $x=-y$ in $x^{2}+y^{2}=36$, we get
$x^{2}+x^{2}=36$
$\Rightarrow x^{2}=18$
$\Rightarrow x=3 \sqrt{2} \mathrm{~m}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
