Question:
The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with horizontal, then the length of the wire is
(a) 12 m
(b) 10 m
(c) 8 m
(d) 6 m
Solution:
Let 
be the length of wire
.
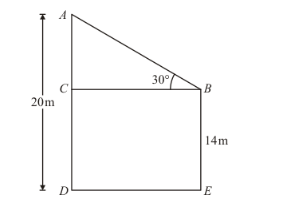
Given that wire makes an angle 
Now, $A C=(20-14) \mathrm{cm}=6 \mathrm{~cm}$,
Here, we have to find length of wire.
So we use trigonometric ratios.
In a triangle
,
$\Rightarrow \sin B=\frac{A C}{A B}$'
$\Rightarrow \sin 30^{\circ}=\frac{6}{h}$
$\Rightarrow \frac{1}{2}=\frac{6}{h}$
$\Rightarrow h=12$
Hence the correct option is a