The towers of bridge, hung in the form of a parabola, have their tops 30 m above the roadway, and are 200 m apart.

Given: Top of the towers are 30 m above the roadway and are 200 m apart. Cable is 5 m above the roadway at center.

Need to find: Length of the vertical supporting cable, 30 m from the center.

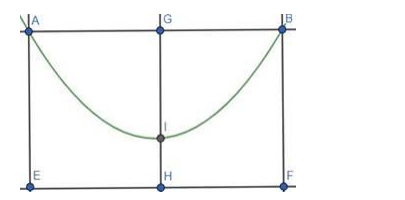
$\mathrm{A}$ and $\mathrm{B}$ are the top of the towers. $\mathrm{AE}$ and $\mathrm{BF}$ are the height of the towers. $\mathrm{H}$ is the center of the bridge. HI is the $5 \mathrm{~m}$ above from the roadway.

Let, the equation of the parabola be: $x^{2}=4 a(y-b)$

Here $b=5 .$ So, $x^{2}=4 a(y-5)$

Here, $A B=200 \mathrm{~m}$ and $B F=30 \mathrm{~m}$.

So, the coordinate of the point $B$ is $(100,30)$

The point is on the parabola.

Hence, $x^{2}=4 a(y-5)$

$\Rightarrow 10000=4 \mathrm{a}(30-5)$

$\Rightarrow 10000=4 \mathrm{a} \times 25$

$\Rightarrow \mathrm{a}=100$

Now we need to find, the length of the vertical supporting cable, $30 \mathrm{~m}$ from the center.

The $x$-coordinate of the point, $30 m$ from the center, is 30 .

So, $30 \times 30=4 a(y-5)$

$\Rightarrow 900=400(y-5)$

$\Rightarrow y-5=\frac{9}{4}$

$\Rightarrow y=\frac{9}{4}+5=\frac{29}{4}$

So, the length of the vertical supporting cable is $\frac{29}{4} m=7.25 m$