The zeroes of the quadratic polynomial x2 + kx + k

(a)Let            p(x) = x2 + kx + k, k≠0

On comparing p(x) with ax2 + bx + c, we get

$a=1, b=k$ and $c=k$

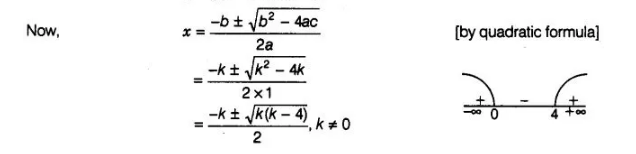
Here, we see that

k(k − 4)> 0

⇒                       k ∈ (-∞, 0) u (4, ∞)

Now, we know that

In quadratic polynomial ax2 + bx + c

If a > 0, b> 0, c> 0 or a< 0, b< 0,c< 0,

then the polynomial has always all negative zeroes.

and if a > 0, c < 0 or a < 0, c > 0, then the polynomial has always zeroes of opposite sign

Case I If                          k∈ (-∞, 0) i.e., k<0

⇒                      a = 1>0,   b,c = k<0

So, both zeroes are of opposite sign.

Case II If                         k∈ (4, ∞)i.e., k≥4

=>                       a = 1> 0,  b,c>4

So, both zeroes are negative.

Hence, in any case zeroes of the given quadratic polynomial cannot both be positive.