There are two types of fertilizers F1 and F2.

Let the farmer buy $x \mathrm{~kg}$ of fertilizer $F_{1}$ and $y \mathrm{~kg}$ of fertilizer $F_{2}$. Therefore,

$x \geq 0$ and $y \geq 0$

The given information can be complied in a table as follows.

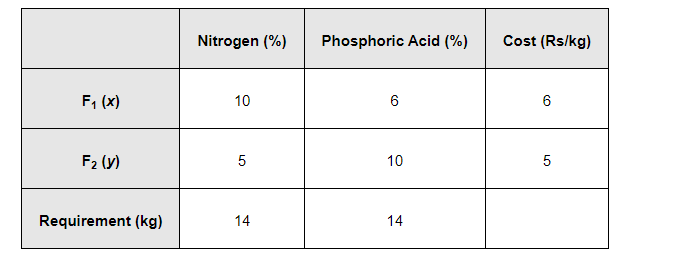
$F_{1}$ consists of $10 \%$ nitrogen and $F_{2}$ consists of $5 \%$ nitrogen. However, the farmer requires at least $14 \mathrm{~kg}$ of nitrogen.

$\therefore 10 \%$ of $x+5 \%$ of $y \geq 14$

$\frac{x}{10}+\frac{y}{20} \geq 14$

$2 x+y \geq 280$

$\mathrm{F}_{1}$ consists of $6 \%$ phosphoric acid and $\mathrm{F}_{2}$ consists of $10 \%$ phosphoric acid. However, the farmer requires at least $14 \mathrm{~kg}$ of phosphoric acid.

$\therefore 6 \%$ of $x+10 \%$ of $y \geq 14$

$\frac{6 x}{100}+\frac{10 y}{100} \geq 14$

$3 x+56 y \geq 700$

Total cost of fertilizers, $Z=6 x+5 y$

The mathematical formulation of the given problem is

Minimize $Z=6 x+5 y$                      (1)

subject to the constraints,

$2 x+y \geq 280 \ldots$ (2)

$3 x+5 y \geq 700 \ldots$ (3)

$x, y \geq 0 \ldots$ (4)

The feasible region determined by the system of constraints is as follows.

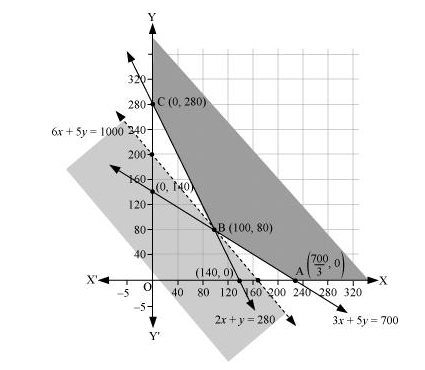
It can be seen that the feasible region is unbounded.

The corner points are $\mathrm{A}\left(\frac{700}{3}, 0\right), \mathrm{B}(100,80)$, and $\mathrm{C}(0,280)$

The values of Z at these points are as follows.

As the feasible region is unbounded, therefore, 1000 may or may not be the minimum value of $Z$.

For this, we draw a graph of the inequality, $6 x+5 y<1000$, and check whether the resulting half plane has points in common with the feasible region or not.

It can be seen that the feasible region has no common point with

$6 x+5 y<1000$

Therefore, $100 \mathrm{~kg}$ of fertiliser $F_{1}$ and $80 \mathrm{~kg}$ of fertilizer $F_{2}$ should be used to minimize the cost. The minimum cost is Rs 1000 .